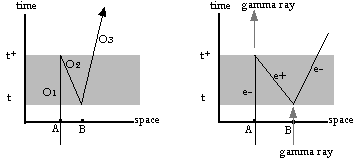
A. Representing Time Travel in Spacetime Diagrams: Special Relativity. What would the worldline of a time traveler look like? Lewis and Harrison both speak of the time traveler as taking a "zigzag" line through spacetime. Compare the following two diagrams (similar to the ones on pages 155-156 of Paul Nahin's book Time Machines).

The diagram on the left represents the worldline of a time traveler named Oscar. Oscar is at location A until t*, when he steps into a time machine and travels back in time to t, steps out of the machine and walks away from point B. An external observer would see three Oscars from t to t* Two Oscars (#2 and #3) would appear spontaneously at B, and move apart. Oscar #2 (designated by O2) would annihilate Oscar #1 at t*, after which only Oscar #3 would exist. Oscar #2 would behave very strangely: his activities would occur in "reverse order." Some illumination into this situation can be gained by considering the diagram at right. We can describe this as the spontaneous creation from a gamma ray of an electron-positron pair at B at t. The positron annihilates the electron at A, creating another gamma ray. As Feynman has said, we can also describe this as a single electron sitting at A until t*, traveling back in time to t, and then traveling forward in time from there. This is possible because reversing the time direction of an electron reverses its charge: hence Feynman's expression that a positron is an electron "traveling backwards in time." Paul Nahin explains the point as follows.
Nahin, page 155: "Just as momentum and space are complementary variables (momentum conservation is the consequence of space direction invariance in the laws of physics) and just as a particle can reverse its direction of motion in space if it loses enough momentum, so a particle can reverse its direction of motion in time if it loses enough energy. This follows because energy and time are another pair of complementary variables. (Conservation of energy is the consequence of time-direction invariance in the laws of physics.)"
Generalizing this point to Oscar as a whole, we could say that from the point of view of an external observer, Oscar #2 is an antimatter version of Oscar #1. There are several problems with this way of understanding Oscar's worldline, however. First, the matter-antimatter Oscar #1-#2 collision would have to release an enormous amount of energy (equivalent to billions of gamma rays). Second, parts of Oscar #1 would have to "tunnel" through parts of Oscar #2 as they joined into one thing before annihilation. Third, this way of looking at things creates problems for identity, in that Oscar can (to put it roughly) be at three places at the same time. Finally, the sharp turns in the world lines (necessary to keep Oscar traveling at less than the speed of light) are problematic, since they involve discontinuities.
B. Representing Time Travel in Spacetime Diagrams: General Relativity. For reasons such as these, "General relativity seems to offer more hope than special relativity to the proponent of time travel" (Earman 1967). There are in fact solutions to Einstein's field equations that allow for "closed timelike curves," i.e., curves in spacetime that are continuous, can represent a causal process in time, and that loop back on themselves. Closed timelike curves would obviously allow for backwards time travel of a sort not plagued by the discontinuities exhibited in the spacetime diagrams above. Mathematician Kurt Gšdel was one of the first people to discover such a solution. In his solution, if the universe were infinite, nonexpanding, and were rotating at a certain rate, the forward light cones would bend forward in the direction of rotation until at a certain critical distance from the center of rotation, they would create a closed timelike loop around the perimeter of rotation. In such a universe, "a traveler can move around a circular path on a trip into his local future and end up in his own global past without ever traveling faster than light" (Nahin, Tech Note 8). As Nahin points out, if a universe with a mass like ours were as Gšdel describes, it would have to rotate once every 70 billion years, and the critical radius for the creation of closed timelike curves would be 16 billion light-years from the center of rotation. (Our universe is nothing like this, of course.) Tipler has recently suggested a variant of this view that describes how one could create closed timelike curves using a rotating, infinitely long cylinder. One could spiral around the cylinder backwards in time, until one reached any point in the past one desired (except points in time before the creation of the cylinder, of course). (See diagram on page 339 of Nahin's Tech Note 8, handed out in class.)
C. Wormholes as Time Machines. Of course, such time machines, though in some sense physically possible (they are consistent with the equations of general relativity), are not of much practical interest, since our universe is expanding and not rotating (against what is required for Gšdel's solution) and there are no infinitely long cylinders available for us to spin (against what is required for Tipler's solution). Kip Thorne has investigated a different strategy, specifically, whether wormholes could be used as time machines. A wormhole is a "handle" or "tunnel" in the topology of spacetime, which connects two widely separated spacetime regions. For example, consider the wormhole diagrams on page 342 of Nahin's Tech Note 10 (handed out in class), or on page 495 of the Thorne reading.
In this example, one could use a wormhole to travel between two spatially separated regions much quicker than could be done by traveling directly through ordinary spacetime. (To use Thorne's example, one could travel from Earth to Vega, 26 light-years away, in a very short amount of time by using a wormhole only 1 kilometer long.) Wormholes have been recognized as physical possibilities for decades, but were not considered to be of much interest since they were believed to be extremely unstable. Thorne has investigated whether wormholes could be made stable, and could be used as time machines. The latter point is easier to deal with, so we will begin there. Recall the Twin Paradox from Special Relativity. Because of time dilation, if Twin A accelerates in a rocket away from Earth, reaches very high speeds relative to the speed of light, and then returns to Earth, he will find Twin B (who has stayed at home) to be much older than he is, even though they were born on the same date! From A's point of view, the rocket was a one-way time machine into the future. The duration and speed of A's journey determines how far into the future he travels. (As noted earlier, time-travel into the future is neither physically nor conceptually problematic, though for various reasons--e.g.., it would take an enormous amount of energy to accelerate to near-light speeds--it will most likely remain a practical impossibility for a very long time.) We can make the trip into the future arbitrarily large by increasing the speed and the duration of the journey. Now, if we consider the two mouths of a wormhole as being like the twins, then accelerating mouth A of the wormhole in a rocketship away from mouth B and then returning would mean that a clock within mouth A would indicate an earlier time than clocks in the surrounding external space, say 9 am and 11 am, respectively. If we keep the wormhole at the same length during our trip (which can in principle be done), then clocks within the wormhole will not have moved relative to one another and so will read the same time. Since mouth B has not moved with respect to the surrounding space, clocks within mouth B would read the same as both the clock within mouth A and those in the surrounding external space, namely 9 am. Thus, you could travel in a rocket in external space from mouth B to mouth A, travel through the wormhole from A to B, and travel to the same spot earlier in time compared to when you left! (This assumes that the round trip takes less time from the traveler's point of view than the time interval separating the two mouths of the wormhole; this can in principle be accomplished since one can vary the speed and duration of mouth A's trip at will.) Of course, one could not travel back in time beyond the moment when the wormhole was first created, so using a wormhole time machine would have its limits.
This raises two issues. First, how would one either find or create a wormhole? Second, how might one keep the wormhole stable enough to travel through it? The second problem is especially acute, since an analysis published by Wheeler and Fuller in 1962 seemed to indicate that a wormhole would collapse so quickly that not even a photon could traverse it! We will deal with this problem below. As for the first question, Morris, Thorne, and Yurtsever (1988) suggested that an infinitely advanced civilization could enlarge one of the microscopic wormholes that form spontaneously in the "quantum foam," and keep it stable by threading its walls with matter or fields with enormous negative (outward) tension. One problem that emerges is that, since the mouth of the wormhole has to "flare out" in order to connect smoothly the with surrounding spacetime, the average energy density of the material holding the wormhole open would in certain reference frames (such as that of a light beam traversing the wormhole) be negative. Such matter (or a field) is called "exotic." Morris, Thorne, and Yurtsever suggested using a device much like one first suggested by Dutch physicist Casimir in 1948 to create a field with negative energy density along the walls of the wormhole, by using a device that permits only certain electromagnetic vacuum fluctuations (see Nahin, Tech Note 10). Morris, Thorne, and Yurtsever calculated that a field of this sort could be used to hold open the wormhole, preventing it from collapse.
The field of the sort investigated by Casimir is one that emerges from the electromagnetic vacuum fluctuations at the quantum level. One worry is whether electromagnetic beams would "pile up" on top of one another at one of the wormhole's mouths, building up enough energy to destroy the wormhole. Thorne rejected one such suggestions involving ordinary light. Light leaving one mouth could travel through space, enter the other mouth of the wormhole, travel back in time, radiate out again in space towards the other mouth, and so on, building up on itself and growing in intensity. The reason that light does not build up according to Thorne is that the mouth of a wormhole acts as a defocusing lens. However, the electromagnetic vacuum fluctuations might be more worrisome. Thorne's initial calculations suggested that these fluctuations would be dispersed but would then refocus while returning to the other mouth. He then calculated that the buildup of these electromagnetic fluctuations would have infinite intensity only for an instant. The laws of quantum gravity say that there is a limit to how small a time interval can exist, so if the buildup occurs for less than this "smallest" time interval, it would not be a problem. Thorne and Kim argued that the buildup would be too weak to destroy the wormhole, but a suggestion by Hawking that they change reference frames for their calculations suggested that this might not be so. Thorne's current thinking on the matter (see quote below) is that electromagnetic vacuum fluctuations would most likely destroy a wormhole before anything could use it as a time machine, but that we cannot know for sure whether this is true until we more fully understand the theory of quantum gravity.
Thorne (email to lzynda@cco, 6/1/95): "Very recently two physicists named Hiscock and Tanaka have called this claim into question; they have shown that, if the vacuum polarization of some massless field diverges slowly enough at a chronology horizon, then giving the field a finite rest mass or making it self-interacting can cut off the divergence, permitting a time machine to activate. It may be that this saves the machine and permits backward time travel for very specially designed machines, but I'm somewhat dubious. I suspect that such salvation requires an original vacuum divergence that is too weak; i.e., I suspect that in all real situations the divergence is so strong that it cannot be counteracted in the Hiscock-Tanaka way --- but it remains an open question. We won't really know the answer until we have mastered the laws of quantum gravity."